Uniform distribution#
1. Theory#
The uniform distribution is the simplest type of continuous probability distribution. The uniform distribution for a continuous random variable is defined by a constant probability density over an interval [a,b].
The probability density function (PDF) of the continuous uniform distribution is:
\(f(x)=\left\{\begin{matrix} \frac{1}{b-a} & \mathrm{for} \, a\leq x\leq b, \\ 0 & \mathrm{for} \, x < a \, \mathrm{or} \, x> b \end{matrix}\right. \)
The cumulative distribution function (CDF) is:
\(F(x)=\left\{\begin{matrix} 0 & \mathrm{for} \, x < a \\ \frac{x-a}{b-a} & \mathrm{for} \, a\leq x\leq b, \\ 1 & \mathrm{for} \, x> b \end{matrix}\right.\)
The mean or expected value of the uniform distribution is given by:
\(E\left [ X \right ] = \frac{b+a}{2 }\)
The variance is: \(\mathrm{Var}\left [ X \right ] = \frac{(b-a)^{2}}{12 }\)
2. Waiting time#

A master’s student of TU Delft takes up a taxi to travel from university and home. The duration of the wait time of the taxi from the pickup point ranges from five to fifteen minutes. Please answer the following questions:
Plot the corresponding PDF and CDF graphs.
What is the probability that the student would have to wait exactly 5 minutes?
What is the probability that the student would have to wait at least 9.5 minutes?
What is the probability that a student would have to wait more than 5.8 minutes?
1. Plot the corresponding PDF and CDF graphs
The duration of the wait time of the taxi from the pickup point ranges from five to fifteen minutes. Therefore, the two constants are \(a=5\) and \(b=15\). A graph of the PDF looks like this:
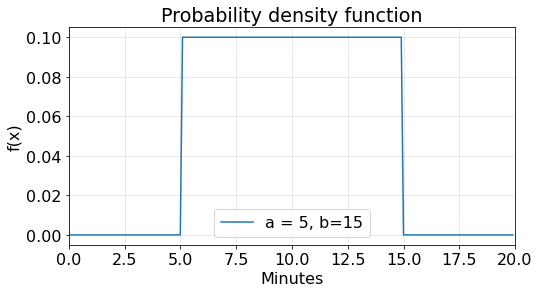
Notice that the probability density function \(f(x)\) is portrayed as a rectangle where the base is \(b-a\) and the height is \(\frac {1}{b-a}\). The area under \(f(x)\) between the endpoints \(a\) and \(b\) is 1.
The plot of the cumulative distribution function CDF of a uniform random variable with \(a=5\) and \(b=15\) is:
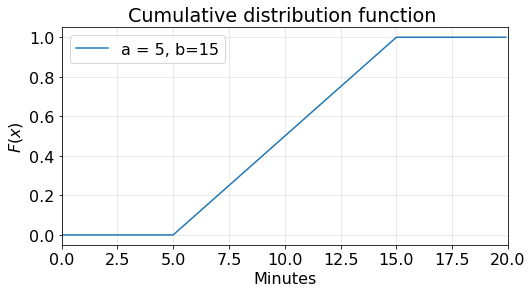
Notice that the slope of the line between \(a=5\) and \(b=15\) is \(\frac {1}{b-a}\).
2. What is the probability that the student would have to wait exactly 5 minutes?
\(P(X=5)=0\)
The probability that a continuous random variable equals some value is always zero.
3. What is the probability that the student would have to wait at least 9.5 minutes?
The duration of the wait time of the taxi from the pickup point ranges from five to fifteen minutes. Therefore, the two constants are \(a=5\) and \(b=15\)
Then, we are asked to solve for \(x \leq 9.5\). Therefore, we need to use the CDF of the uniform distribution:
\(P(X \leq x) = \frac{x-a}{b-a}\)
\(P(X \leq 9.5) = \frac{9.5-5}{15-5}= 0.45\)
Therefore, the probability that the student would have to wait at least 9.5 minutes is 45%
We can easily obtain the solution using the following Python script:
#interval [a,b]
a = 5
b = 15
x = 9.5
probability = (x-a)/(b-a) #CDF
#display the result rounded to two decimal places
print(f'The probability is {probability:.2f}')
The probability is 0.45
4. What is the probability that a student would have to wait more than 5.8 minutes?
We are asked to solve for \(x > 5.8 \):
\( P(X > x) = 1 - \frac{x-a}{b-a}\)
\( P(X > 5.8) = 1 - \frac{5.8-5}{15-5}= 0.92\)
Therefore, the probability that the student would have to wait at least 5.8 minutes is 92%
We can easily obtain the solution using the following Python script:
#interval [a,b]
a = 5
b = 15
x = 5.8
probability = 1 - ((x-a)/(b-a)) #CDF
#display the result rounded to two decimal places
print(f'The probability is {probability:.2f}')
The probability is 0.92
3. Total vehicle length#

The traffic manager agency of the Dutch motorway A12 has received the results of last month’s Weight in Motion (WIM) system measurements. Assume the total vehicle length of a randomly chosen 4-axle truck (T11O3 according to the WIM vehicle codification) is a uniformly distributed random variable ranging from 12.9 m to 15.8 m.
Please answer the following:
The following plots show three Uniform probability density functions of the total vehicle length:
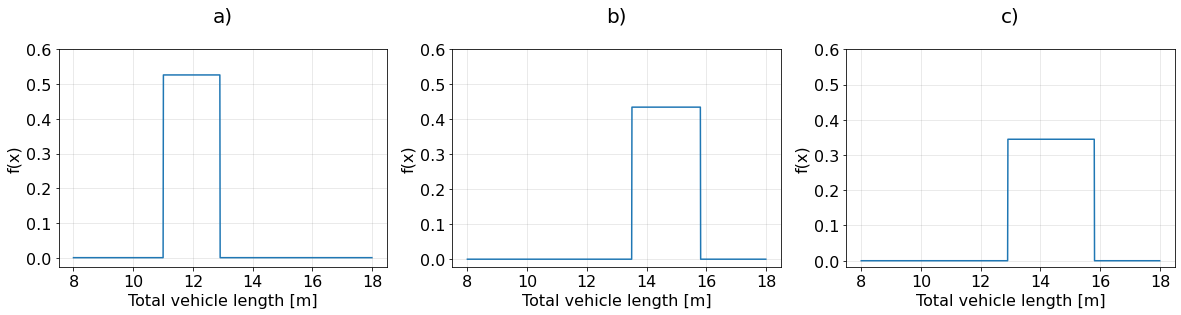
Important!
Answer all questions in three decimal places and review the “Waiting time” example questions and answers to help you answer these questions.
Determine whether each statement is TRUE or FALSE
