Bernoulli distribution#
1. Theory#
Bernoulli distribution
Let \( X \) be a discrete random variable with two possible outcomes, \(x=0\) and \(x=1\). The one and zero are arbitrary and used to represent the two possible outcomes in a simple way; sometimes one of these values is also defined as failure. The Bernoulli distribution is commonly used when there are two outcomes of a trial (success or failure) and the probability of success is equal to \(p\) (in this case we define success as \(x=1\)).
There are three important assumptions required to be able to apply the Bernoulli Distribution in practice:
Each trial has exactly two possible outcomes.
The probability of success (p) is the same across all trials.
Each trial is independent.
Based on these assumptions, we can write an equation that gives the probability of all possible outcomes of \(x\) (there are only two!). Such an equation is called a probability mass function (PMF) because it describes how probability is allocated to all possible values of \(x\). The PMF of the Bernoulli distribution is derived as a function of \(x\) and \(p\) as follows:
\(p_{X}(x)=P(X=x)=p^x(1-p)^{1-x} \quad \textrm{for} \quad x = 0,1 \)
Where \(p\) is the parameter that denotes the probability of a successful outcome. We can see that this PMF is quite simple for the Bernoulli case as \(x\) can only take on a single value which simplifies the equation. The reason we write out the PMF here is because later we will see that the Bernoulli Distribution is a special case of the Binomial Distribution, specifically: the case of a single trial.
2. Student population#

According to TU Delft Facts and Figures, approximately 4 in 9 students are enrolled at the TU Delft master’s program. One student is randomly selected.
What is the distribution of the number of master’s students?
What is the probability that we do get one master’s student?
What is the probability that we do not get one master’s student?
1. What is the distribution of the number of master’s students?
We got a single trial, each student is a master’s student, or they are not. Hence the conditions of a Bernoulli distribution here are satisfied. So, the number of master’s students is going to have a Bernoulli distribution with parameter \(p = 4/9\).
If we let the random variable (X) be the number of master’s students in our sample size 1. The distribution of the number of master’s students is:
\( P(X=x) = \left ( \frac{4}{9} \right )^{x}\cdot \left (1-\frac{4}{9}\right )^{1-x} \)
for \(x=0,1\) because we are going to get a master’s student (1) or not (0).
2. What is the probability that we do get one master student?
From question 1 we know that if we get a master’s student, then \(x=1\). By substituting the value of \(x=1\) into the obtained equation from question 1, one can determine the probability associated with the event of obtaining a single master’s student as follows:
\( P(X=x) = \left ( \frac{4}{9} \right )^{1}\cdot \left (1-\frac{4}{9}\right )^{1-1} = \frac{4}{9} = 0.444\)
Hence, the probability that we do get one master’s student is about 44.4%
To answer this question we can use the following Python script:
p = 4/9
x = 1
probability = p**x*(1-p)**(1-x)
#displays the result rounded to three decimal places
print(f'The probability is {probability:.3f}')
The probability is 0.444
3. What is the probability that we do not get one master’s student?
Here, by ‘do not get one master’s student’ it means that \(x=0\). If we substitute \(x=0\) in the equation obtained from question 1, we get:
\( P(X=0) = \left ( \frac{4}{9} \right )^{0}\cdot \left (1-\frac{4}{9}\right )^{1-0} = \frac{5}{9} = 0.556\)
Hence, the probability that we do not get one master’s student is about 55.6%
To answer this question we can use the following Python script:
p = 4/9
x = 0
probability = p**x*(1-p)**(1-x)
#displays the result rounded to three decimal places
print(f'The probability is {probability:.3f}')
The probability is 0.556
That’s it! Note that this was a pretty simple set of exercises because the Bernoulli is a very simple distribution. We used the PMF to make our calculations, but you should also be able to go back and see how the answers could have been determined directly using the ratio of master’s students in each case.
Now let’s test this knowledge on a new problem!
3. International master’s student population#
According to TU Delft Facts and Figures, the total student population enrolled at the TU Delft master’s program is 13029 of which 4356 are international students. One master’s student is randomly selected.
Please answer the following:
Important!
All answers need to be provided in three decimal places.
The following plots show three Bernoulli probability mass functions of the number of international master’s students. From left to right plot a, plot b and plot c:
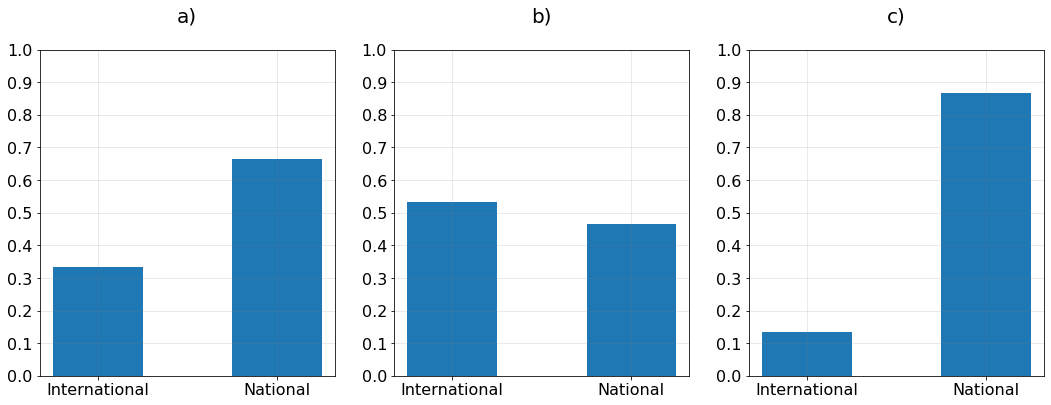
Determine whether each statement is TRUE or FALSE
