Poisson distribution

Poisson distribution#

1. Theory#

In a Poisson distribution, the following assumptions are always satisfied:

The random variable, \( X \), is the number of times an event occurs during a defined interval. The interval can be time, distance, area, volume, or some similar unit.
The probability of occurrence is the same for any 2 intervals of equal length, i.e. the rate of occurrence is constant.
The occurrence or non-occurrence in any interval is independent of the occurrence or non-occurrence in any other interval.
Two events cannot occur at exactly the same time.
The events do not occur in clusters and the chance of finding an object in a particular location (or time) is not the same as finding it elsewhere.

The homogeneous Poisson probability mass function is given by:

\(p_{X}(x)=P(X=x)=\frac{\nu ^{x}}{x!}\mathrm{exp}(-\nu) \quad \mathrm{for} \: x=0,1,2,...\)

Where:

\(p_{X}(x)= P(X=x)\) is probability of \(x\) occurrences in an interval.

\(\nu\) is considered to be the mean number of arrivals or happenings in an interval.

2. Reliability of equipment at a pump station#

All the pumps at a pump station have been made to the same specifications by a single manufacturer. From tests conducted over a 6-week period, it has been ascertained that there are on average two breakdowns during each period. It is assumed that the failures occur randomly in time, the occurrences are independent, and the rate of failure is constant.

What is the probability that the water treatment plant will have exactly three breakdowns over 6 weeks?
A new plant manager assumes that the problem is not serious if there are no more than five breakdowns over 6 weeks. What is the probability of such an occurrence?
The water treatment plant would close for repairs if there were more than 7 breakdowns. The plant manager assumes that the probability of that happening is less than 0.10. Is this correct?

1. What is the probability that the water treatment plant will have exactly two breakdowns over 6 weeks?

There are on average three breakdowns during each period, i.e. \(\nu = 3\)

We need to ﬁnd the probability that the water treatment plant will have exactly two breakdowns, i.e. \(x = 2\).

By using the homogeneous Poisson probability mass function: \(P(X=2) = \frac{3 ^{2}}{2!}\mathrm{exp}(-3)\)

Thus, \(P(X=2) = 0.224\)

The probability that the water treatment plant will have exactly two breakdowns over 6 weeks is 0.224 or 22.4%

We can easily obtain the solution using the following Python script:

import numpy as np  #import numpy library to use factorial and exponential functions
nu = 3
x = 2
probability = nu**x/np.math.factorial(x)*np.exp(-nu)

#display the result rounded to three decimal places
print(f'The probability is {probability:.3f}') 

The probability is 0.224

2. A new station manager assumes that the problem is not serious if there are no more than five breakdowns over 6 weeks. What is the probability of such an occurrence?

We are being asked for \(P(X \leq 5)\). The homogenous Poisson model is applicable with parameter \(\nu =3\) and \(P(X\leq5) = \sum_{x=0}^{5}\frac{3^{x}}{x!}\mathrm{exp}(-3)\) \(P(X\leq5) = 0.0498 + 0.1494 + 0.224 + 0.224+ 0.168 + 0.1008 = 0.916\)

The probability that there are no more than five breakdowns over 6 weeks is 0.916 or 91.6%

We can easily obtain the solution using the following Python script:

import numpy as np #import numpy library to use factorial and exponential functions
nu  = 3
x = [0,1,2,3,4,5]
probability = sum([nu**breakdown /np.math.factorial(breakdown)*np.exp(-nu) 
                   for breakdown in x])

#display the result rounded to three decimal places
print(f'The probability is {probability:.3f}') 

The probability is 0.916

3. The water treatment plant would close for repairs if there are more than 7 breakdowns. The manager assumes that the probability of that happening is less than 0.10. Is this correct?

We are being asked for \(P(X>7)\). The homogenous Poisson model is applicable with parameter \(\nu =3\) and \( P(X>7) =1 - P(X \leq 7) = 1 - \sum_{x=0}^{7}\frac{3^{x}}{x!}\mathrm{exp}(-3) \)

By using the following Python script:

import numpy as np #import numpy library to use factorial and exponential functions
nu  = 3
x = [0,1,2,3,4,5,6,7]
probability = 1 - sum([nu**breakdown /np.math.factorial(breakdown)*np.exp(-nu) 
                       for breakdown in x])

#display the result rounded to three decimal places
print(f'The probability is {probability:.3f}')  

The probability is 0.012

The probability of more than 7 breakdowns is 0.012. The plant manager is therefore justified in his assumption.

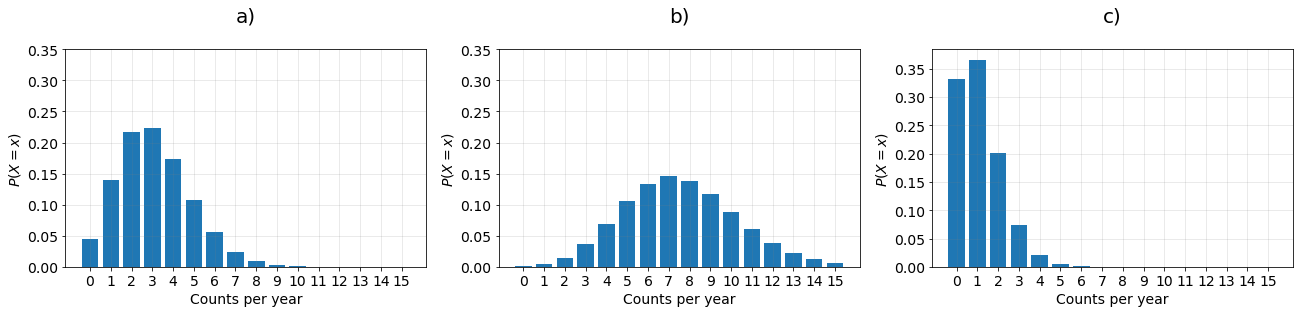
3. Hurricanes#

According to the U.S. National Oceanic and Atmospheric Administration on average there are 7.6 hurricanes per year (based on data from 2000 to 2021). Assume that the hurricane events are independent and the number of times an event occurs in an interval follows a Poisson distribution.

Please answer the following:

The following plots show three probability mass functions, from left to right respectively; plot a, plot b and plot c:

Important!

Please round all answers to three decimal places.