Exercises#
Note
You don’t need to worry about using Interactive Jupyter Notebooks for these exercises. You can simply ignore the rocket icon () and go ahead to answer the questions using the knowledge you’ve gained from the chapter. Have fun!
Exercise 1.2.2#
What is the type of the result of the following expression \(3 + 1.5 + 4?\)
strintfloat
Exercise 1.2.3#
What is the index of the letter ’r’ of the sentence ’Hello engineer!’
(Fixing) Exercise 1.2.4#
In the following exercise you will be using a piece of code, which was written by other people. It can contain concepts you haven’t encountered yet but you need to practice with using code you don’t understand completely. This is because you want to be able to use programs written by other people. Just like with calculators — if you add two numbers you get the result you expect to get. But you don’t know exactly how that piece of plastics with electronic components performs that calculation.
In order to approach the problem, start from the point of error. If your error cannot be solved there, work your way backwards through the code. Only try to understand the parts that are necessary to fix your problem, and avoid changing parts you know that work.
There are 2 types of numbers in Python: integer numbers and floating point numbers. Both have overlapping and different applications. For example, counting rocks will require only integers (1 rock, 2 rocks, 3 rocks, etc), while their weight can be expressed in both int and float (depending on the required accuracy).
In the code cell below you can see a small dataset of the measured daily temperatures and a filter function, which is used to remove incorrect measurements. A student wanted to indicate the position of the erroneous measurement, so it can be later filtered out during data analysis. However, when using the filter function, filter_errors, the erroneous measurement it wasn’t removed. The filter function is known to work flawlessly (no errors there), meaning that the mistake happened in the indication step. It is known that the corrupted sample is the 5th in the dataset (5th because the first element has index 0! Python has a zero-based indexing).
temperature_dataset = [12.0, 13.5, 11.0, 12.7, 670.5, 11.8] # in Celsius
def filter_errors(dataset, error_id):
print('Data before filtering', dataset)
del dataset[error_id - 1]
return print('Data after filtering', dataset)
filter_errors(temperature_dataset, 5.0)
(Searching) Exercise 1.2.5#
There are also other data types in Python, which were not mentioned in this part (in case they are not as useful or will be introduced later). For instance, Complex is one of them. The sad truth is that every software developer Googles a lot. It’s not because she/he is lazy or incompetent. It is because programming languages are constantly updated and some tools are limited to a narrow field of applications. It is impractical to learn everything at once, therefore every coder has learned how to look up the functionality their task requires. Therefore, it is crucial for you to learn how to Google as well. Complex type is used in Python to represent complex numbers. If you haven’t heard about them — a complex number is a number, which has a real and an imaginary part. For example, \(x = 17 + 5i\). Here, \(x\) is a complex number with a real part of \(17\) and an imaginary part of \(5\).
Your task is to create a variable my_complex_number of Complex type and assign a \(3 + 2i\) value to it. For that you will have to Google a bit. Try to look for something like “Python complex variables”. Python is very popular and you will be able to find everything you need. Make sure to filter the information you need — not everything you will find will be useful for this simple exercise.
What is the correct my_complex_number variable?
my_complex_number = 3 + 2imy_complex_number = 3 + 2jmy_complex_number = 3 + 2k
Exercise 1.3.1#
Given that we have a rectangle with a height of \(3\) cm, width of \(5\) cm and a cutout circle of radius \(0.6\) cm, as shown below.
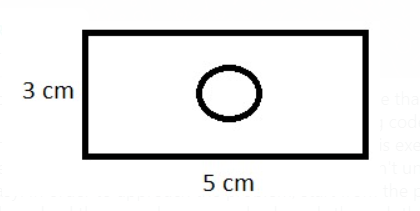
In the code cell bellow you will find a script that computes the remainder area. However there is a mistake in the code.
rectangle_height = 3
rectangle_width = 5
pi = 3.14159265359
radius = 0.6
circle_area = pi * radius * 2
rectangle_area = rectangle_height * rectangle_width
remaining_area = rectangle_area - circle_area
print(f'The remaining area is {remaining_area:.2f} cm^2')
Exercise 1.3.2#
Suppose a group of \(5\) engineers ordered \(4\) pizzas with \(8\) slices each.


