Example System
Example System#
A pre-fabricated bridge design is being considered for river crossings in a remote region of the world, as shown in Figure 1. Cities 1, 2 and 3 are labelled C1, C2 and C3, with bridges labelled B1-B4.
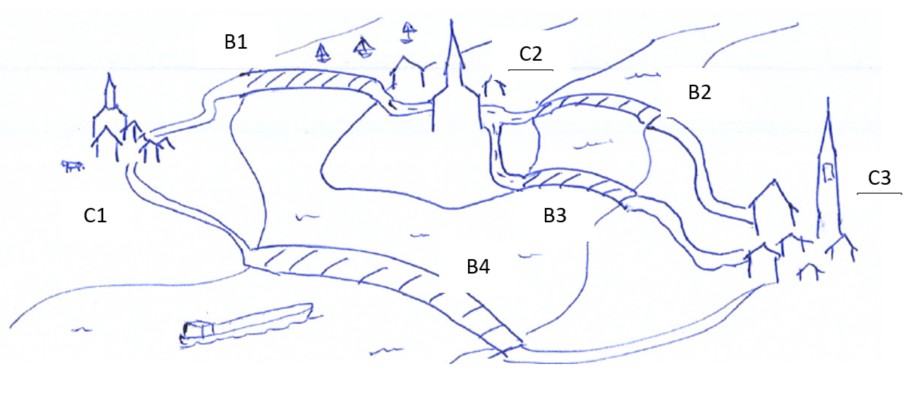
Question 1: If the probability of failure for an individual bridge is 0.1 per year, compute the probability that you cannot drive from City 1 to City 2
Answer
Question 2: If the probability of failure for an individual bridge is 0.1 per year, compute the probability that you cannot drive from City 2 to City 3.
Answer
Question 3: If the probability of failure for an individual bridge is 0.1 per year, compute the probability that you cannot drive from City 1 to City 3
Answer
Question 4: Suppose there is a critical facility (e.g., a hospital) in City 3. How many bridges would you need to install between City 2 and 3 to ensure that the probability of someone not reaching City 3 from City 2 is less than \(10^{-4}\)?
Answer
It is necessary to install 2 more bridges between City 2 and 3.
Question 5: If you had 1 extra bridge to place, which bridge (i.e., B1, 2, 3 or 4) would you place it next to in order to have the biggest decrease of the probability of not reaching City 3 from City 1?
Answer
I would locate the extra bridge next to Bridge 4. In this case, adding an extra element in the parallel system, making it more redundant.
\(P_f\) next to B1 = 0.00199
\(P_f\) next to B2 or B3 = 0.0101
\(P_f\) next to B4 = 0.00109
Question 6: If you only had 3 available bridges, which of the 4 bridges in the figure would you remove first, to cause the smallest reduction in failure probability?
Answer
I would remove Bridge 2 or 3. If bridge 1 or 4 is removed, a whole path is removed from the system, while by removing only Bridge 2 or 3, there is still an available bridge to cross that river.
Question 7: What should the probability of each bridge be in order to make the probability of not crossing from C1 to C3 less than 0.01?
Answer
Since the bridges have identical designs and have all been manufactured by the same contractor, positive dependence is expected between performance of bridges B1-B4.
Question 8: State whether or not dependence would increase or decrease the probability calculated in question 3, and explain why with 1 or 2 sentences.
Answer
Increase.
The probability of failure would increase because the system mainly works like a parallel system. In this case, when there is full dependence between the elements, the probability of failure equals the probability of failure of the strongest element. For instance, \(P_{f_{\text{bridges 2, 3}}}=0.01\) for independent case and 0.1 for full dependence case.
Assume each prefabricated bridge is made up of a single road deck and 5 separate frames that are joined together. Each bridge will fail if either the road deck fails, or 1 of the frames fails.
Question 9: If the probability of a frame failure is 0.01, what is the required failure probability of the road deck to make sure the bridge failure probability is no more than 0.1?
Answer
